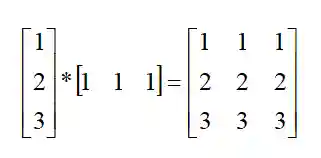线性代数基础知识归纳
条评论知识来源
- 麻省理工公开课 线性代数 (网易公开课)
- 《INTRODUCTION TO LINEAR ALGEBRA》– 作者:GILBERT STRANG (就是麻省理工公开课里的老师所做,此书可淘宝购买影印版)
基础归纳
方程组可以看作 若干向量的线性组合: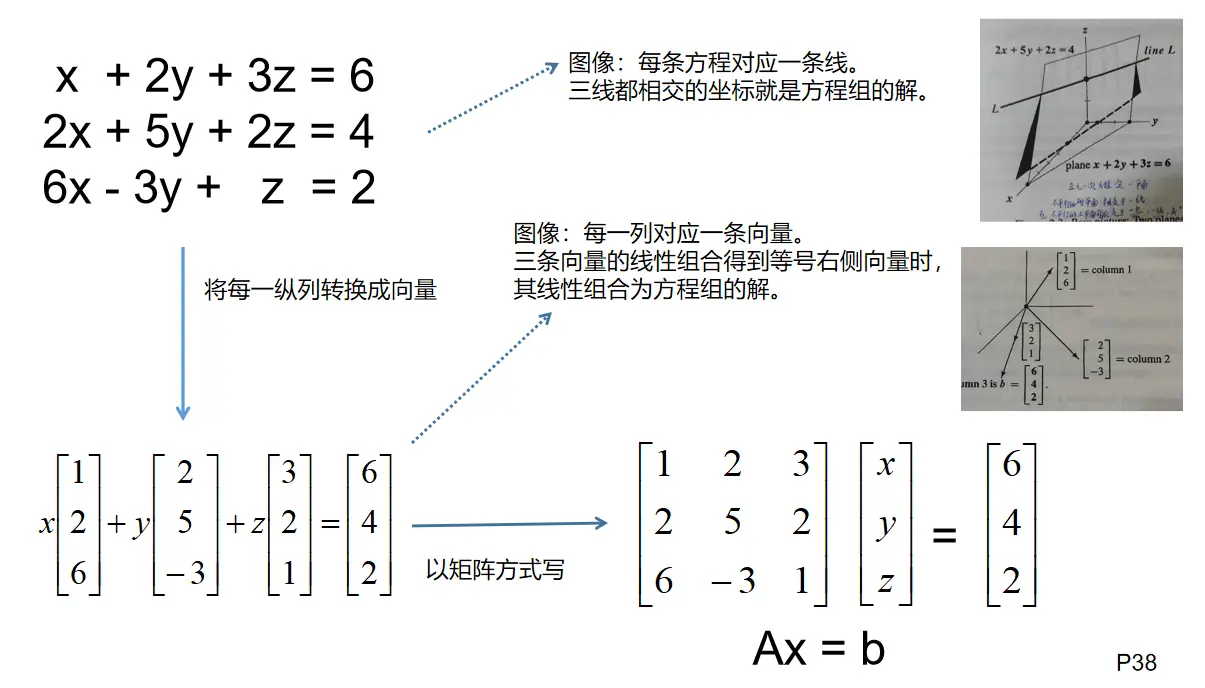
行乘列
A(i,j)代表矩阵A的第i行,第j列的元素。如上面的矩阵 A(3,1) = 6 。
很容易看到,矩阵乘一个向量等于一个向量,记住其对应关系:前面的第一行各元素 分别乘 后面向量的各元素等于 等号右侧的第一个值: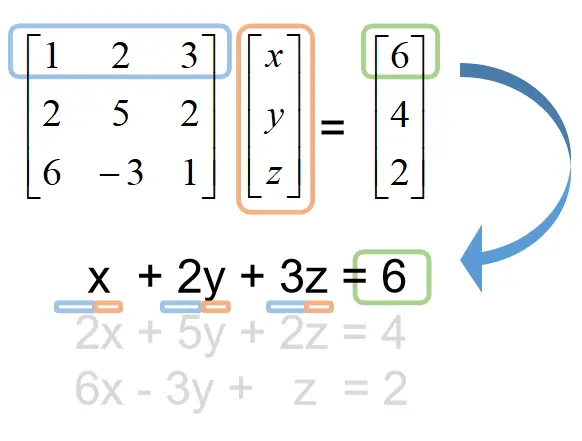
两矩阵相乘(A*B=C),矩阵C(i,j)等于 矩阵A的第i行乘 矩阵B的第j列之和: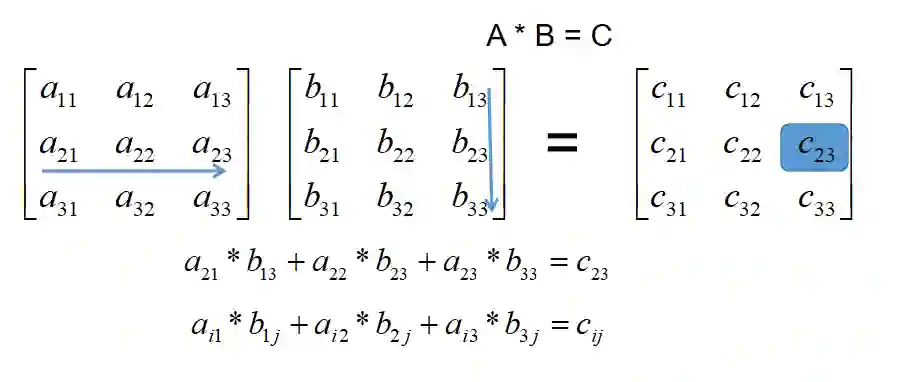
行乘矩阵
将矩阵C第i行看作是矩阵A的第i行 乘 矩阵B的各行,即是B各行的线性组合: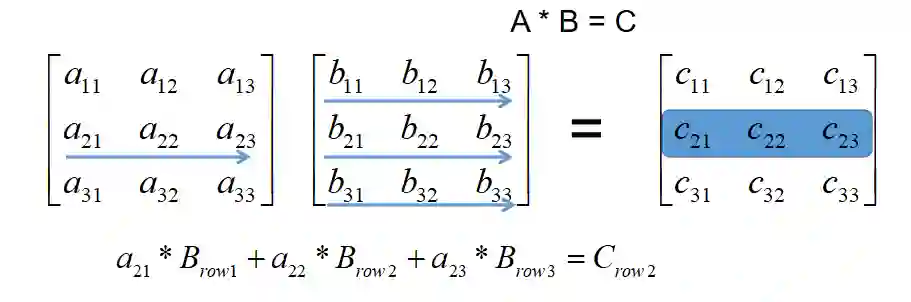
这样子整行计算,会相对直观快速些,举个例子: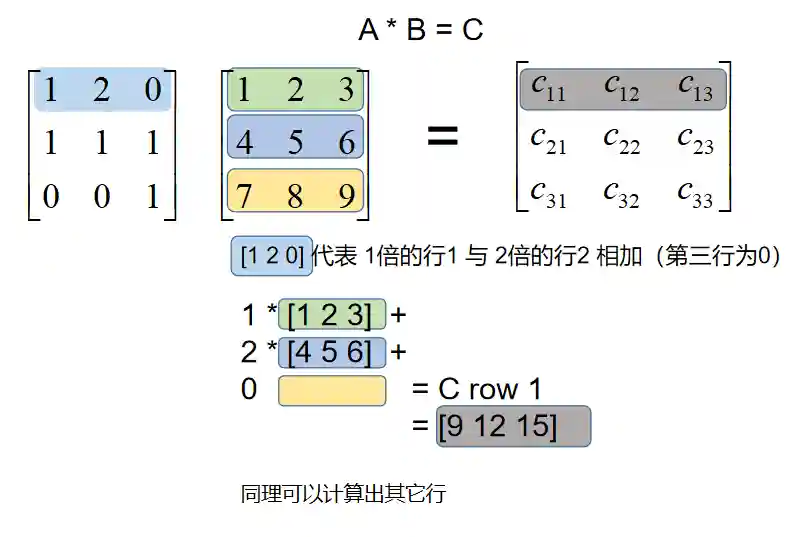
矩阵乘列
也可以将矩阵C 看作 A各列的线性组合: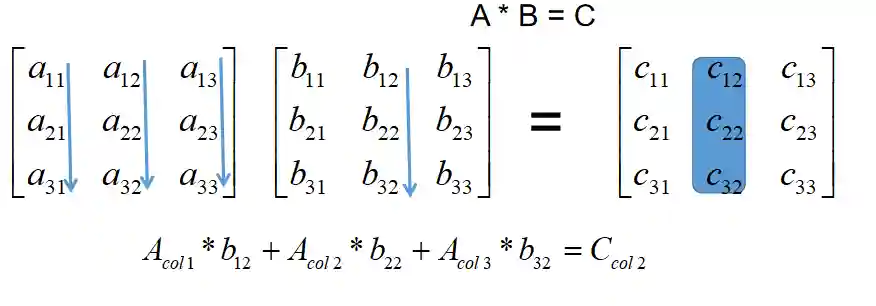
列乘行
最后提一下,列乘行的结果,就是得到一个矩阵。